논문 링크 : https://arxiv.org/abs/2505.12540 코드 : https://github.com/rjha18/vec2vec/

논문 요약#

✅ Problem

• •서로 다른 모델에서 생성된 텍스트 임베딩들은 기하 구조(geometry)가 다르기 때문에 비교가 불가능함.
• •예를 들어, T5 베이스인 GTR, BERT 베이스인 GTE 등 다양한 모델의 임베딩은 같은 문장이라도 전혀 다른 공간에 위치함.
• •기존에 벡터를 비교하려면 쌍(pair) 데이터가 필요했음.
• •즉, 같은 문장 A를 인코더1과 인코더2에서 나온 두 벡터를 비교해서 정렬하는 방식을 써야 함.
• •하지만 벡터 DB만 있고, 어떤 문서에서 어떤 모델 인코더로 변환했는지 모르는 경우에는 벡터 DB가 유출되더라도, 어떤 문서를 의미하는지 파악하기 어려움.

✅ Main Idea / Solution

• •vec2vec : 어떤 모델의 임베딩이든, 쌍 정보나 인코더 없이 보편적 의미 공간(latent space) 을 통해서 번역 가능하게 하자.
• •Strong Platonic Representation Hypothesis를 전제로 함: “같은 목적과 같은 modality로 학습된 신경망은 학습 데이터나 모델 구조가 달라고, 결과적으로 보편적인 의미 공간(universal latent space)으로 수렴하며, 따라서 쌍 정보(pairwise correspondence) 없이도 서로의 표현을 변환하는 임베딩 간 번역이 가능하다”
• •두 모델(M₁, M₂)의 임베딩을 보편적인 latent space로 매핑하고 다시 역변환하는 구조
• •GAN loss + Reconstruction loss + cycle-consistency loss + vector space preservation(VSP)로 의미, 거리, 방향성 모두 보존되는 임베딩 변환 학습

✅ Result

• •vec2vec 변환된 벡터만 가지고도
• •속성 추론 (attribute inference) 성공 (예: 병명, 이메일 주제 등)
• •문장 복원 (zero-shot inversion)도 최대 80% 복원
• •심지어 멀티모달 모델인 CLIP 임베딩에도 적용 가능
• •학습에 쓰지 않았던 out-of-distribution 텍스트(트윗, 의료 데이터)에도 잘 작동

Abstract#

우리는 쌍(pair) 데이터, 인코더, 미리 정해진 매칭 정보 없이도, 한 벡터 공간에서 다른 벡터 공간으로 텍스트 임베딩을 번역하는 최초의 방법을 제안한다. 우리가 제안한 비지도 방식은, 임의의 임베딩을 보편적인 잠재 표현(universal latent representation) 으로 양방향 번역할 수 있다. 우리의 번역 방식은 모델 구조, 파라미터 수, 학습 데이터가 서로 다른 모델 쌍에서도, 높은 코사인 유사도(cosine similarity) 를 달성했다. 임베딩의 기하 구조(geometry)를 보존하면서, 알 수 없는 임베딩을 다른 공간으로 번역할 수 있는 능력은, 벡터 DB의 보안에 심각한 영향을 미칠 수 있다. 벡터DB만 유출돼도, 거기서 문서의 주제나 민감한 정보(질병, 이름 등)를 복원해낼 수 있다는 의미다.

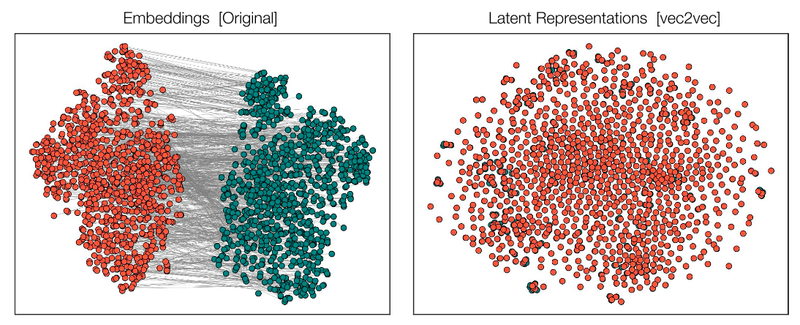
• •왼쪽(Original Embeddings)
  • •빨간 점: 한 모델(GTR), 초록 점: 다른 모델(GTE)에서 생성된 임베딩들.
  • •서로 완전히 다른 위치에 분포하고 있음 → 직접 비교 불가
• •오른쪽 (Latent Representations [vec2vec])
  • •동일한 데이터가 vec2vec을 통해 공통된 latent space로 변환됨.
  • •두 모델에서 나온 임베딩들이 하나의 의미 공간에서 섞여 정렬됨 → 같은 의미를 공유하고 있음

Problem formulation: unsupervised embedding translation#

목표

• •vec2vec을 활용해서 모르는 문서 $d_i$에서 나온 임베딩 벡터만 가지고 정보를 추출해보자.

가정과 우리가 알고있는 것

• •$M_2$인코더 : 우리가 알고 있는 인코더. 즉, 알고 있는 문서에서 임베딩을 추출하는 인코더.
• •문서 $d_i$가 텍스트라는 점과 그리고 이게 어떤 언어인지 정도는 알고 있음.
• •$\{u_1, u_2, \ldots, u_n\}$, $u_i = M_1(di)$ : 모르는 문서 $d_i$에서 모르는 인코더 $M_1$에서 나온 임베딩 벡터
• •$M_1$ 인코더 : 우리가 모르고 있는 인코더. 구조도, 어떤 데이터로 학습했는지도 모름.

기존에 벡터를 비교하려면 쌍(pair)이 필요했음. 즉, 같은 문장 A를 인코더1과 인코더2에서 나온 두 벡터를 비교해서 정렬하는 방식을 썼음. 하지만 이렇게 벡터끼리 쌍을 정렬(alignment, mapping, matching, correspondence) 하던 방식으로는 위와 같은 가정상황에서 쓰일 수 없음. 기존의 문서도 아예 모르고, 어떤 모델(인코더)로 변환되었는지도 모르고 쌍도 없기 때문에!

그럼에도 임베딩 벡터에서 정보를 추출하고 싶음. 그래서 $M_1$과 $M_2$가 생성하는 벡터 공간이 구조적으로 비슷할 것이라는 가정이 필요함. 즉, $M_1$과 $M_2$가 만든 벡터들이 다른 숫자값을 갖더라도, 그 안에 숨어 있는 의미 간 거리 관계는 비슷할 수 있다는 가정을 가지고 시작함.

이 가정은 Platonic Representation Hypothesis(플라톤 표현 가설)에서 기인했음. 플라톤 표현 가설은 충분히 학습한 이미지 모델은 공통된 의미 공간(latent representation)을 가질 것이라는 가설임. 그리고 이 논문에서는 이 가설이 텍스트에서도 적용될 것이라 보았고, 이 플라톤 표현 가설이 이론적 주장에 그치지 않고 실제로 실험을 통해 맞다는 걸 보여주며 Strong Platonic Representation Hypothesis 라고 이름 붙임.

" 같은 목적(objective)과 형태(modality) 로 훈련된 신경망들은, 비록 다른 데이터와 다른 아키텍처를 사용했더라도, 결국에는 공통된(universal) 잠재 공간(latent space) 으로 수렴(converge)하며, 이로 인해 쌍(pairwise correspondence) 정보 없이도 표현 간 변환(translation) 을 학습할 수 있다. "

서로 다른 모델(M1, M2)이라도 충분히 잘 학습되었다면, 결국 같은 의미 구조(latent representation) 를 공유할 것이다 → 그래서 벡터들 사이에 공통 구조가 있을 것이다!

그리고 vec2vec은 이 가정을 믿고 공통된 기하 구조(geometry)만을 단서로 학습함.

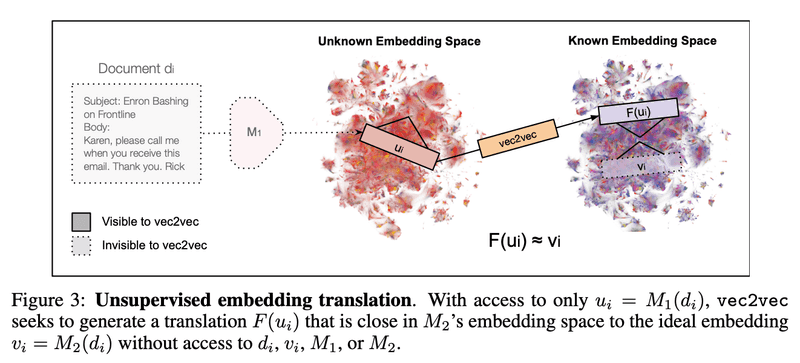
• •위 사진에서 $u_i = M_1(d_i)$는 $M_1$이라는 모르는 모델이 어떤 문서 $d_i$를 임베딩한 결과임.
• •$v_i = M_2(d_i)$는 같은 문서$d_i$를 M2로 임베딩한 결과이고, 이게 목표하는 값임.
• •$F(u_i)$는 vec2vec이 만든 변환 결과로 목표는 $F(u_i) \approx v_i$가 되도록 학습하는 것임.

vec2vec 학습과정#

그럼 이제 vec2vec 이 어떻게 학습되는지 알아보자.

• •목표 : vec2vec, 즉 임베딩 공간 간 변환(embedding-space translations) 을 학습하고자 한다!

이를 학습하기 위해 두 가지 조건을 만족해야 함.

1. 순환 일관성(cycle-consistent)

한 공간에서 다른 공간으로 갔다가 다시 돌아오면, 원래 벡터로 되돌아와야 한다. A 공간 → B 공간 → 다시 A 공간 이렇게 두 변 변환했을 때 다시 원래 벡터로 돌아와야 함 : $u \rightarrow F(u) \rightarrow F^{-1}(F(u)) \approx u$

2. 식별 불가능성(indistinguishable)

같은 텍스트에서 나온 벡터라면, 어느 임베딩 공간($M_1$이든 $M_2$든)에서 오든 동일한 잠재 표현(latent representation) 을 가져야 한다.

Architecture#

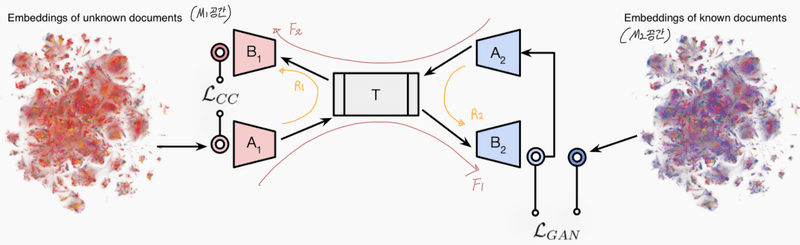
1. Input Adapter (입력 어댑터)

• •역할: 각 모델(M1, M2)의 임베딩을 공통 잠재 공간으로 변환
  • •$A_1 : \mathbb{R}^d \rightarrow \mathbb{R}^Z$, M1 모델에서 나온 벡터를 변환하는 어댑터
  • •$A_2 : \mathbb{R}^d \rightarrow \mathbb{R}^Z$, M2 모델에서 나온 벡터를 변환하는 어댑터

2. Shared Backbone (공통 백본 네트워크)

• •역할: 변환된 벡터에서 공통 의미 표현(latent representation)을 추출
  • •$T : \mathbb{R}^Z \rightarrow \mathbb{R}^Z$

3. Output Adapter (출력 어댑터)

• •역할: 공통 의미 표현을 다시 특정 임베딩 공간 으로 변환
  • •$B_1 : \mathbb{R}^Z \rightarrow \mathbb{R}^d$, M1 모델 임베딩 공간으로 변환하는 어댑터
  • •$B_2 : \mathbb{R}^Z \rightarrow \mathbb{R}^d$, M2 모델 임베딩 공간으로 변환하는 어댑터

주요 함수 정의

• •$F_1 = B_2 \circ T \circ A_1$ (M1 임베딩 → M2 공간으로 변환)
• •$F_2 = B_1 \circ T \circ A_2$ (M2 임베딩 → M1 공간으로 변환)
• •$R_1 = B_1 \circ T \circ A_1$ (M1 임베딩 → 자기 자신 공간으로 재구성)
• •$R_2 = B_2 \circ T \circ A_2$( M2 임베딩 → 자기 자신 공간으로 재구성)

모델의 학습 대상 파라미터 : $\theta = \{A_1, A_2, T, B_1, B_2\}$

vec2vec의 네트워크 구성

• •MLP 기반 네트워크 사용
• •Residual connections: 정보 손실 방지
• •Layer Normalization: 학습 안정화
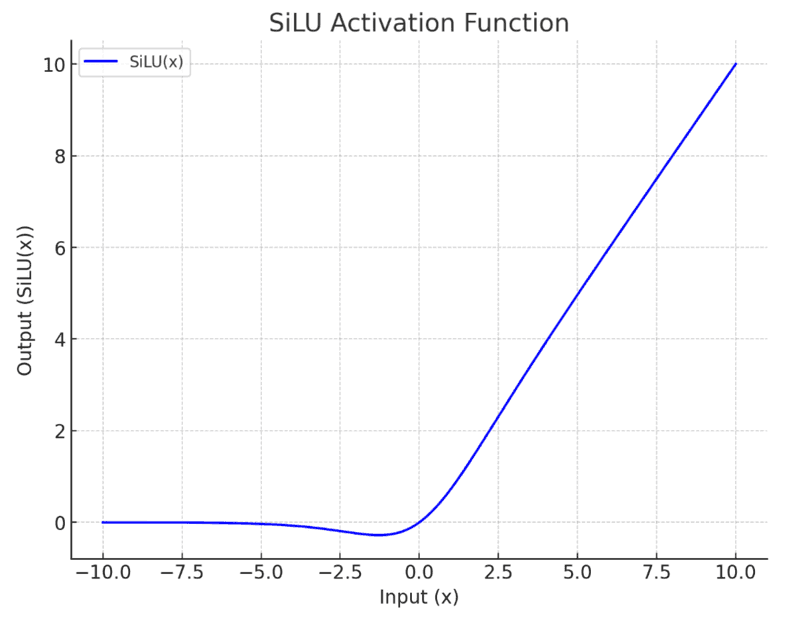
• •SiLU(Swish) activation: ReLU보다 부드러운 비선형 함수

SiLU(Sigmoid Linear Unit, Swish) activation

$\text{SiLU}(x) = x \cdot \sigma(x) = x \cdot \frac{1}{1 + e^{-x}}$

Discriminator

• •판별자(discriminator)도 구조는 비슷하지만, GAN 훈련 시 불안정해지지 않게 하기 위해 잔차 연결은 제거

Optimization#

생성자 네트워크 $F$와 $R$ 외에도, 판별자(discriminator) 를 도입함. $D_{1\ell}$, $D_{2\ell}$는 F의 잠재 표현(latent representation)에 대해 동작하는 판별자, $D_1$, $D_2$는 출력 임베딩에 대해 동작하는 판별자임.

objective function : 우리의 목표는 다음 식을 최적화하는 $\theta$ 를 찾는 것

$\mathcal{L}_{adv}$ : 적대적 손실 (adversarial loss) : 판별자를 속일 수 있는 진짜같은 벡터 생성 능력을 의미. 임베딩 공간과 잠재 공간(latent space) 양쪽 모두에서 생성자가 만든 벡터가 진짜처럼 보이도록 학습시키는 GAN 손실

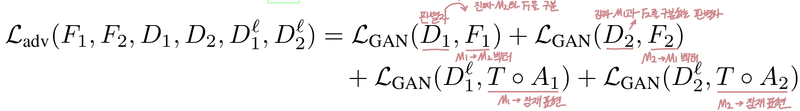
$\mathcal{L}_{gen}$ : 의미 구조를 보존하는 생성자 loss : 적대적 손실만으로는 의미 보존이 되지 않기 때문에, 복원 손실($\mathcal{L}_{rec}$), 순환 일관성 손실($\mathcal{L}_{cc}$, Cycle-consistency Loss), Vector space preservation loss($\mathcal{L}_{vsp}$) 를 도입함. $λ$는 각 항의 중요도를 나타내는 파라미터임.

1. $\mathcal{L}_{rec}$ : 복원 손실(Reconstruction loss)

임베딩을 잠재 공간으로 보낸 뒤 다시 원래 공간으로 복원했을 때, 초기 벡터와 매우 비슷해야 함.

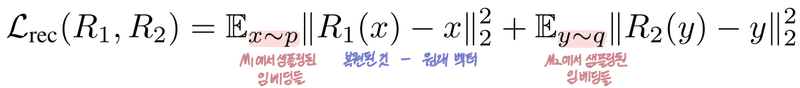
2. $\mathcal{L}_{cc}$ : 순환 일관성 손실(Cycle-consistency Loss)

임베딩을 다른 공간으로 변환했다가 다시 돌아왔을 때, 원래 벡터와 매우 비슷해야 함.

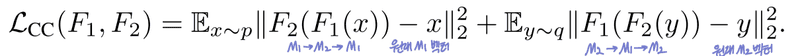
3. $\mathcal{L}_{vsp}$ : (Vector space preservation, VSP Loss)

목적 : 변환된 임베딩 간의 상대적 관계(유사도)를 원래 임베딩과 최대한 비슷하게 만드는 것. 임베딩 간의 의미적 거리 구조(geometry)를 보존하기 위함. 즉, 원래 임베딩에서 벡터들끼리의 유사도와 변환된 임베딩에서 벡터들끼리의 유사도가 비슷해야 함. 이걸 모든 데이터 pairwise로 계산함.

실험 과정 및 결과#

• •훈련/평가 : Natural Questions(NQ, 질문 + 위키 답변) — 학습: 200만개 / 평가: 65536개
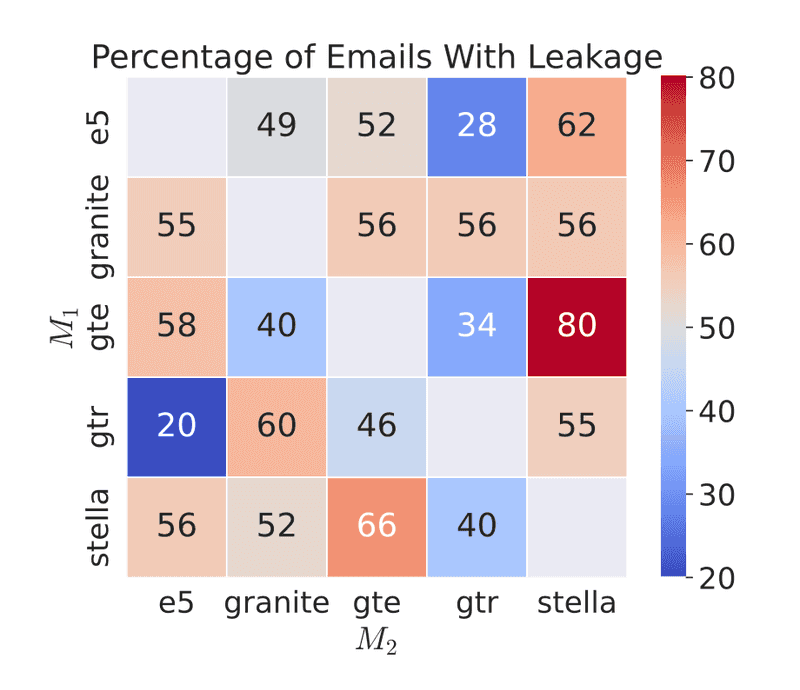
• •정보 추출 평가 : TweetTopic (트윗, 19개 주제 다중 라벨), MIMIC (환자 기록, 질병 2673개 다중 라벨), Enron 이메일 (공개, 레이블 없음, 50개 샘플)

각 vec2vec 모델은 NQ(Natural Questions)에서 추출한 서로 겹치지 않는 100만 개의 64토큰 시퀀스로부터 생성된 두 개의 임베딩 세트를 사용해 학습함. GAN의 불안정성 때문에 여러 초기화 중 가장 성능이 좋은 모델을 선택했고, 보다 안정적인 학습법은 후속 연구로 남겨둠.

같은 back-bone(모델)을 공유하는 임베딩(gte, e5, stella)끼리는 vec2vec의 성능이 나이브 기준선, 오라클 기준선과 비슷함. 그러나 back-bone이 다른 경우에는 vec2vec의 성능이 다른 기준선에 비해 월등히 높은 것을 볼 수 있음.

vec2vec은 Wikipedia 기반의 NQ 데이터셋으로 학습되었지만, 평가에 쓰인 트윗 데이터(더 구어체이고 이모지를 사용함), 의료 기록 데이터(NQ에는 나오지 않는 전문 용어가 많음) 처럼 도메인이 다른 데이터셋에서도 높은 성능을 보여줌. 예를 들어, 훈련 데이터에 한 번도 등장하지 않았던 질병 이름인 “alveolar periostitis” 같은 개념도 vec2vec의 latent space에서 의미 정보를 잘 보존하고 있다는 것은 vec2vec이 진정한 보편 표현(universal representation)을 학습했다는 강력한 증거가 됨.

이러한 결과는 vec2vec이 새로운 modality에도 적용할 수 있는 가능성을 보여줌. 특히 CLIP은 이미지 외에도 히트맵, 오디오, 차트 같은 다양한 모달리티와 성공적으로 연결된 사례가 있음.

$M_1$은 원래 임베딩을 생성한 모델, $M_2$는 vec2vec이 번역한 목표 임베딩 공간으로, 각 숫자는 번역 후 임베딩으로부터 원래 내용을 어느정도 복원했는지의 비율을 보여줌. gte 임베딩을 stella로 번역한 경우, GPT-4o는 80%의 이메일에서 정보가 드러났다고 판단함.

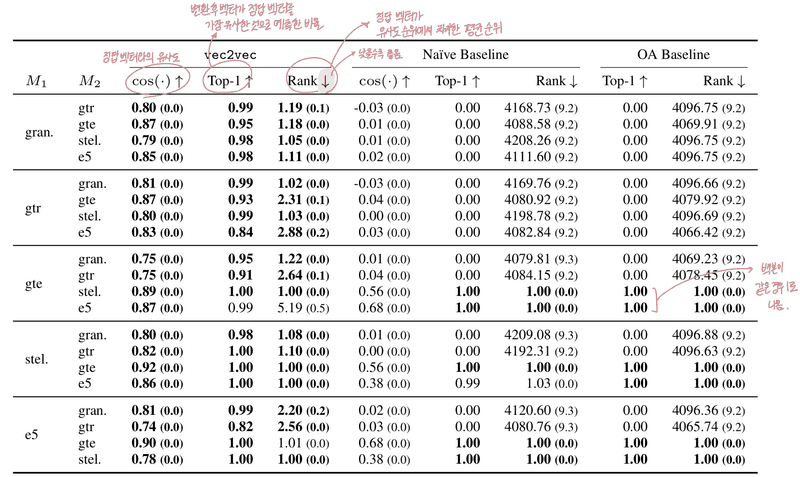
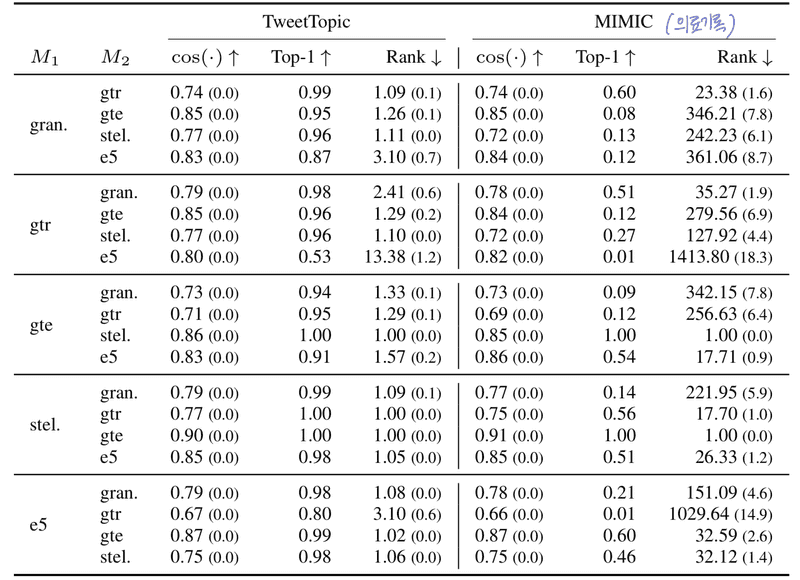
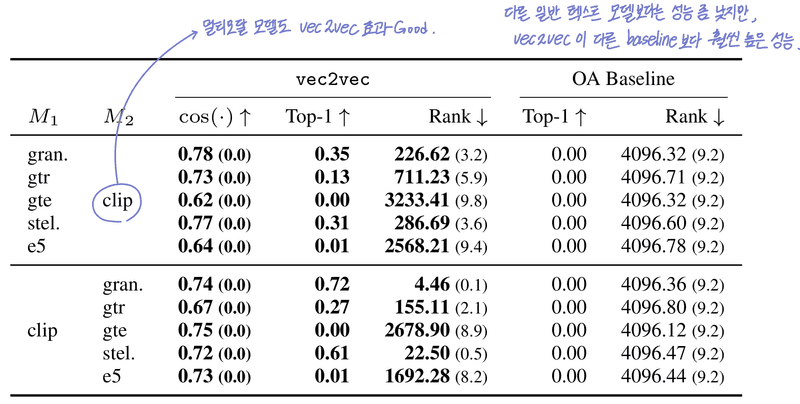
• •Zero-shot Inversion: 임베딩 → 다시 텍스트를 복원하려는 시도 (텍스트 생성)
• •Zero-shot: 사전 학습된 inversion 모델을 그대로 사용함 (fine-tuning 없음)
• •목표: 임베딩만으로 원래 문서의 내용이 얼마나 드러나는지를 측정
• •결과 : 복원은 완벽하진 않지만, 인물, 회사 이름, 날짜, 금융 정보, 프로모션, 심지어 점심 주문 정보까지 복원 가능. vec2vec은 단순히 벡터 공간을 매핑하는 수준이 아니라, 의미 수준에서도 정보를 상당히 잘 보존한다는 강력한 증거. 이로 인해 임베딩만 공개되더라도 정보가 유출될 수 있음을 보여주는 실험.

결론#

vec2vec은 보편적인 의미 공간을 학습하여, 사전 정의된 매칭이나 인코더 없이도 다양한 표현 공간 간 의미 보존 및 번역이 가능함을 보여주며, 이는 표현 공간 간 통합을 가능케 하는 강력한 이론적, 실용적 기반을 제공함.